 N . (A
dense matrix is a matrix in which most of the entries are nonzero.) This
matrix-matrix multiplication involves
N . (A
dense matrix is a matrix in which most of the entries are nonzero.) This
matrix-matrix multiplication involves 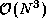 operations, since
for each element
operations, since
for each element 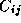 of C , we
must compute
of C , we
must compute
![[DBPP]](4_6 Case Study Matrix Multiplication.files/asm_color_tiny.gif)





![[Search]](4_6 Case Study Matrix Multiplication.files/search_motif.gif)
In our third case study, we
use the example of matrix-matrix multiplication to
illustrate issues that arise when developing data
distribution neutral libraries. In particular, we consider the problem of developing a library to compute C = A.B
, where A , B , and C are dense matrices of size
N  N . (A
dense matrix is a matrix in which most of the entries are nonzero.) This
matrix-matrix multiplication involves
N . (A
dense matrix is a matrix in which most of the entries are nonzero.) This
matrix-matrix multiplication involves 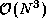 operations, since
for each element
operations, since
for each element 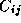 of C , we
must compute
of C , we
must compute

We wish a library that will allow each of the arrays A , B , and C to be distributed over P tasks in one of three ways: blocked by row, blocked by column, or blocked by row and column. This library may be defined with a subroutine interface suitable for sequential composition in an SPMD program or with a channel interface suitable for parallel or concurrent composition. The basic algorithmic issue remains the same: Does the library need to incorporate different algorithms for different distributions of A , B , and C , or should incoming data structures be converted to a standard distribution before calling a single algorithm?
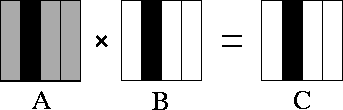
Figure
4.10: Matrix-matrix multiplication A.B=C with matrices
A , B , and C decomposed in one dimension. The
components of A , B , and C allocated to a single
task are shaded black. During execution, this task requires all of matrix
A (shown stippled).
We start by examining algorithms for various distributions of A , B , and C . We first consider a
one-dimensional, columnwise decomposition in which each task encapsulates
corresponding columns from A , B , and C . One
parallel algorithm makes each task responsible for all computation associated
with its 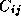 . As shown in Figure
4.10,
each task requires all of matrix A in order to compute its
. As shown in Figure
4.10,
each task requires all of matrix A in order to compute its 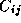 .
. 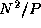 data are required from each of P-1 other tasks, giving the following
per-processor communication cost:
data are required from each of P-1 other tasks, giving the following
per-processor communication cost:
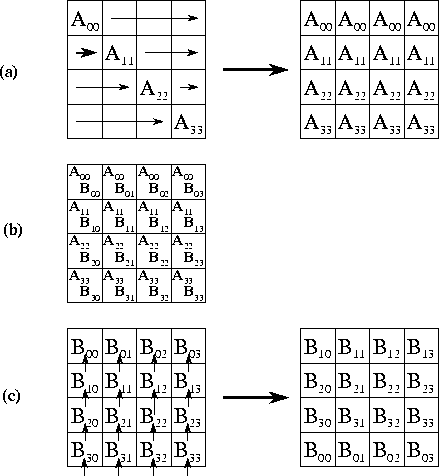
Note that as each task performs 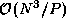 computation, if
N
computation, if
N 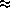 P , then
the algorithm will have to transfer roughly one word of data for each
multiplication and addition performed. Hence, the algorithm can be expected to
be efficient only when N is much larger than P or the cost of
computation is much larger than
P , then
the algorithm will have to transfer roughly one word of data for each
multiplication and addition performed. Hence, the algorithm can be expected to
be efficient only when N is much larger than P or the cost of
computation is much larger than 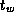 .
.
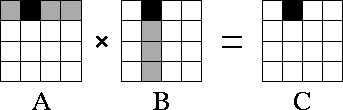
Figure
4.11: Matrix-matrix multiplication A.B=C with matrices
A , B , and C decomposed in
two dimensions. The components of A , B , and C
allocated to a single task are shaded black. During execution, this task
requires corresponding rows and columns of matrix A and B ,
respectively (shown stippled).
Next, we consider a two-dimensional decomposition of A , B
, and C . As in the one-dimensional algorithm, we assume that a task
encapsulates corresponding elements of A , B , and C
and that each task is responsible for all computation associated with its 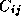 . The computation of
a single element
. The computation of
a single element 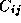 requires an entire
row
requires an entire
row 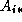 and column
and column 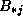 of A and
B , respectively. Hence, as shown in Figure 4.11, the
computation performed within a single task requires the A and
B submatrices allocated to tasks in the same row and column,
respectively. This is a total of
of A and
B , respectively. Hence, as shown in Figure 4.11, the
computation performed within a single task requires the A and
B submatrices allocated to tasks in the same row and column,
respectively. This is a total of 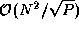 data, considerably
less than in the one-dimensional algorithm.
data, considerably
less than in the one-dimensional algorithm.
Figure
4.12: Matrix-matrix multiplication algorithm based on
two-dimensional decompositions. Each step involves three stages: (a) an
A submatrix is broadcast to other tasks in the same row; (b) local
computation is performed; and (c) the B submatrix is rotated upwards
within each column.
To complete the second parallel algorithm, we need to design a strategy for communicating the submatrices between tasks. One approach is for each task to execute the following logic (Figure 4.12):
for j
=0 to
in each row i
, the
accumulate
send
endfor
set
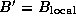
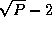
 th task broadcasts
th task broadcasts
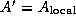 to the other tasks in the row
to the other tasks in the row
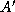 .
.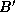
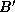 to upward neighbor
to upward neighbor
Each of the 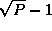 steps in this
algorithm involves a broadcast to
steps in this
algorithm involves a broadcast to 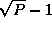 tasks (for
A' ) and a nearest-neighbor communication (for B' ). Both
communications involve
tasks (for
A' ) and a nearest-neighbor communication (for B' ). Both
communications involve 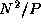 data. Because the
broadcast can be accomplished in
data. Because the
broadcast can be accomplished in 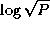 steps using a tree
structure, the per-processor communication cost is
steps using a tree
structure, the per-processor communication cost is
Notice that because every task in each row must serve as the root of a broadcast tree, the total communication structure required for this algorithm combines a hypercube (butterfly) structure within each row of the two-dimensional task mesh and a ring within each column.
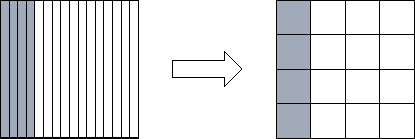
Figure
4.13: Reorganizing from a one-dimensional to a one-dimensional
decomposition of a square matrix when P=16. Shading indicates one set of
four tasks that must exchange data during the reorganization.
Comparing Equations 4.3 with 4.4, we see that the two-dimensional decomposition yields the
more efficient parallel algorithm. Does this mean that our parallel library
should convert input arrays decomposed in one dimension to a two-dimensional
decomposition before performing the matrix multiplication? To answer this
question, we need to know the cost of the reorganization. The communication
costs associated with the reorganization of a single array are as follows; each
task exchanges data with 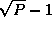 other tasks, with
each message having size
other tasks, with
each message having size 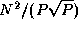 (Figure 4.13):
(Figure 4.13):
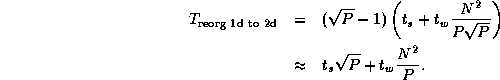
If A , B , and C are all decomposed in one dimension, we must perform three such conversions. This gives a worst-case total communication cost for reorganization and multiplication using the two-dimensional algorithm of
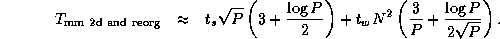
Comparing this expression with Equation 4.3, we see that the algorithm that reorganizes data structures to a 2-D decomposition before performing the multiplication will be more efficient than an algorithm that does not, when
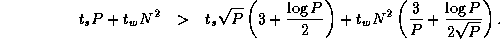
This condition holds for all except small P . Hence, we conclude that our parallel matrix multiply library should convert to a two-dimensional decomposition before performing computation, as follows.
procedure matrix_multiply(A, B, C)begin
if 1d_distributed(A) then reorg_to_2d(A)
if 1d_distributed(B) then reorg_to_2d(B)
2d_matrix_multiply(A, B, C)
if 1d_distributed(C) then reorg_to_1d(C)
end
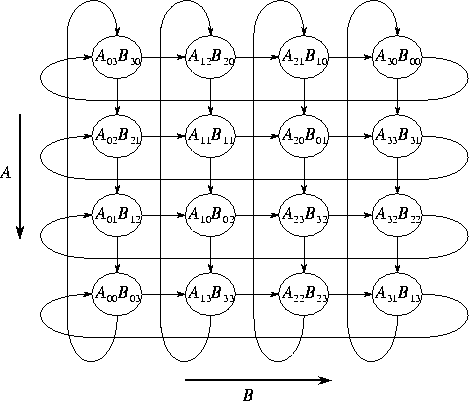
Figure
4.14: Layout of the A and B matrices in the
systolic matrix-matrix multiplication algorithm for a 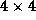 task mesh.
The arrows show the direction of data movement during execution of the systolic
algorithm.
task mesh.
The arrows show the direction of data movement during execution of the systolic
algorithm.
We still have not said the last word about the ideal data distribution for
matrix-matrix multiplication! An alternative algorithm
allows the broadcast operations used in the preceding algorithm to be replaced with regular, nearest-neighbor (``systolic'')
communications. However, data must be distributed among tasks in a different
fashion. As before, we assume that A , B , and C are
decomposed into 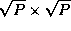 submatrices. Each
task (i,j) contains submatrices
submatrices. Each
task (i,j) contains submatrices 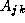 ,
, 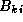 ,
and
,
and 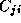 , where
, where 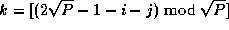 . This data layout
is illustrated in Figure 4.14.
. This data layout
is illustrated in Figure 4.14.
Computation proceeds in 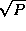 steps. In each
step, contributions to C are accumulated in each task, after which
values of A move down and values of B move right. The entire
computation requires a total of
steps. In each
step, contributions to C are accumulated in each task, after which
values of A move down and values of B move right. The entire
computation requires a total of 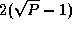 messages per task,
each of size
messages per task,
each of size 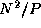 , for a cost of
, for a cost of

Communication costs are less by a factor of about 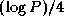 than in
Equation 4.4.
Again, this benefit must be weighed against the cost of converting matrices
A , B , and C into the layout required by this
algorithm. This analysis is left as an exercise.
than in
Equation 4.4.
Again, this benefit must be weighed against the cost of converting matrices
A , B , and C into the layout required by this
algorithm. This analysis is left as an exercise.
![[DBPP]](4_6 Case Study Matrix Multiplication.files/asm_color_tiny.gif)





![[Search]](4_6 Case Study Matrix Multiplication.files/search_motif.gif)
© Copyright 1995 by Ian Foster