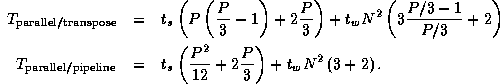![[DBPP]](4_4 Case Study Convolution.files/asm_color_tiny.gif)





![[Search]](4_4 Case Study Convolution.files/search_motif.gif)
Next: 4.5
Case Study: Tuple Space Up: 4
Putting Components Together Previous: 4.3
Performance Analysis
In the remainder of this chapter, we apply the
modular design techniques discussed in preceding
sections in three case studies. We start with an example
from image processing, which we use to study design
tradeoffs that can arise when constructing parallel
programs from several components. We consider the problem of applying a series of convolution operations to a
sequence of images. Images, represented as arrays of size N  N , are input in
pairs on streams A and B ; convolution generates a new array
of the same size that is output on stream C (Figure 4.4). A
single convolution operation involves the transformation of two input arrays
using independent two-dimensional fast Fourier transforms (2-D FFTs), a
pointwise multiplication of the two transformed arrays, and the transformation
of the resulting array using an inverse 2-D FFT, thereby generating an output
array. A 2-D FFT performs 1-D FFTs first on each row and then on each column of
an array. A 1-D Fourier transform,
N , are input in
pairs on streams A and B ; convolution generates a new array
of the same size that is output on stream C (Figure 4.4). A
single convolution operation involves the transformation of two input arrays
using independent two-dimensional fast Fourier transforms (2-D FFTs), a
pointwise multiplication of the two transformed arrays, and the transformation
of the resulting array using an inverse 2-D FFT, thereby generating an output
array. A 2-D FFT performs 1-D FFTs first on each row and then on each column of
an array. A 1-D Fourier transform, 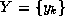 , of a sequence of N
values,
, of a sequence of N
values, 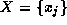 , is given by
, is given by
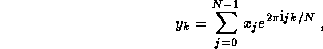
where 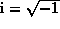 . The FFT exploits symmetry to
perform this computation in
. The FFT exploits symmetry to
perform this computation in 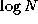 steps, each involving
steps, each involving 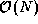 operations.
operations.
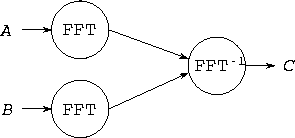
Figure
4.4: Dataflow diagram for an image-processing pipeline. Two streams
of images, A and B , are passed through FFT modules and then
into an inverse FFT module, which first multiplies them and then applies an
inverse FFT.
We first consider the three components from which the
convolution algorithm is constructed: forward 2-D FFT, multiplication, and
inverse 2-D FFT. The pointwise multiplication is the simplest: Its communication
requirements are zero as long as the arrays on which it operates have the same
data distribution.
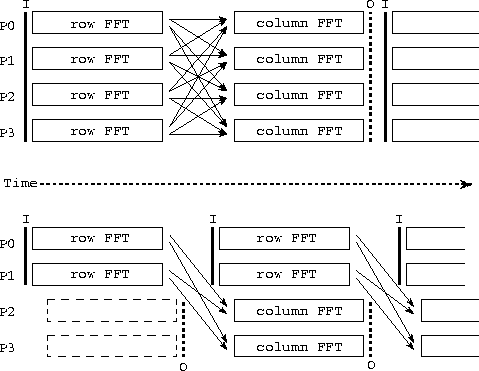
Figure
4.5: Two parallel algorithms for computing a series of 2-D FFTs. In
each case, the activity on each of four processors (P0--3) is shown over time,
with arrows denoting communication and I and O denoting input and output
operations. The algorithm illustrated in the upper part of the figure is a
sequential composition of program components that perform 1-D FFTs, first on
rows and then on columns of each input 2-D array; all-to-all communication is
required to transpose the array after performing row FFTs and before performing
column FFTs. In the second algorithm, data flow from a first set of processors
performing row FFTs (P0, P1) to a second set performing column FFTs (P2, P3).
Communication is required to move data from P0 and P1 to P2 and P3.
A variety of parallel algorithms are possible for the forward and inverse 2-D
FFTs. A fine-grained algorithm can exploit concurrency within the 1-D FFTs
performed on individual rows and columns of the input array, at the cost of
considerable communication. A more coarse-grained algorithm performs independent
1-D FFTs in parallel, thereby avoiding a need for communication within the 1-D
FFTs, but requiring communication when moving from a row-based to a column-based
decomposition. We consider two algorithms based on the latter strategy. The
first processes the input image stream sequentially, performing row FFTs and
then column FFTs on each image in turn. The second algorithm pipelines the image
stream, performing column FFTs for one image in parallel with the row FFTs for
the next (Figure 4.5).
These two algorithms are in effect sequential and parallel compositions,
respectively, of code fragments that perform 1-D FFTs on the rows and columns of
a two-dimensional array.
The first parallel algorithm is termed the
transpose algorithm, since it performs a series
of one-dimensional transforms on P processors
while the array is partitioned in one dimension, then transposes the array and
performs transforms in the second dimension using the same processors. The
transpose operation requires that each processor send one message of size 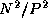 to each of the P-1 other processors. Hence, total communication costs
summed over P processors are
to each of the P-1 other processors. Hence, total communication costs
summed over P processors are
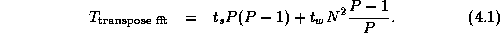
The second algorithm is termed the pipeline
algorithm, since it partitions processors into two sets of size
P/2 which perform FFTs on rows and columns, respectively. Each
processor in the first set must communicate with each processor in the other
set, for a total of 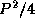 messages. The entire array is
communicated. Hence, total communication costs are
messages. The entire array is
communicated. Hence, total communication costs are
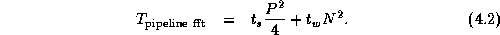
Notice that communication costs are not necessarily distributed equally among
processors in the second algorithm, since the sending and receiving processors
form distinct groups. Nevertheless, Equations 4.1 and 4.2 give a
rough idea of the relative performance of the two algorithms. The second
algorithm sends significantly fewer messages and hence should be more efficient
in situations in which message startup costs are dominant, for example, when
N and/or 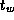 are small or when P
or
are small or when P
or 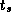 are large. On the other hand,
the first algorithm probably incurs lower data transfer costs and hence may be
superior in other situations.
are large. On the other hand,
the first algorithm probably incurs lower data transfer costs and hence may be
superior in other situations.
Having designed two alternative algorithms for the 2-D FFT, we now consider the parallel convolution algorithm proper. Its
four components---two parallel 2-D FFTs, one matrix
multiplication, and one inverse 2-D FFT (Figure 4.4)---can
be combined using either sequential or parallel composition. If sequential
composition is used, the parallel convolution algorithm can be represented as
follows, with the fft and fft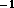 calls invoking the
transpose 2-D parallel FFT.
calls invoking the
transpose 2-D parallel FFT.
for each image
A = fft(A)
= fft(A)
B = fft(B)
= fft(B)
C = A
= A .B
.B
C = fft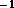 (C
(C )
)
endfor
If the input to this algorithm is decomposed appropriately (in one dimension,
by rows), then because each FFT involves a transpose, total communication
requirements are three times the cost of a single transpose:
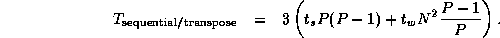
Notice that because the forward FFT operates first on rows and then on
columns, the inverse FFT must operate first on columns and then on rows, so as
to avoid the need for an additional transpose operation between the forward and
inverse FFTs.
If parallel composition is used, the three FFTs execute concurrently, each on
one third of the available processors. (Because the
multiplication involves 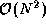 rather than
rather than 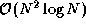 operations, we regard it as insignificant and compose it
sequentially with the inverse FFT.) Communication costing
operations, we regard it as insignificant and compose it
sequentially with the inverse FFT.) Communication costing 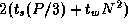 is required
to move data from the processors handling the forward FFTs to the processors
handling the inverse FFT.
is required
to move data from the processors handling the forward FFTs to the processors
handling the inverse FFT.
The 2-D FFTs within the parallel composition can be implemented by using
either the transpose or pipeline algorithms, yielding two algorithm variants.
Costs are as specified by Equations 4.1 and 4.2, except
that each algorithm is executed three times, with P/3 rather than
P processors involved in each execution. Combining these costs with the
cost of the data movement between components, we obtain the following models.
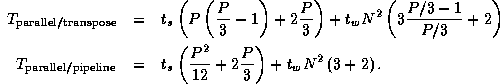
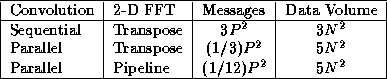
Table
4.1: Approximate total message counts and data volumes for three
parallel convolution algorithms, summed over P processors and assuming
that P is reasonably large.
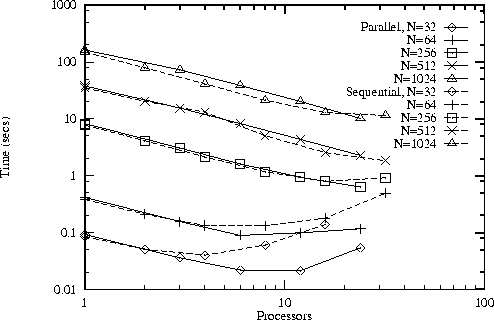
Figure
4.6: Performance of the sequential/transpose (Sequential) and
parallel/transpose (Parallel) convolution algorithms on an IBM SP computer for
different problem sizes and numbers of processors. The latter algorithm is more
efficient for smaller problems and larger numbers of processors.
The results of this brief analysis are summarized in Table 4.1. We
see that the second and third algorithms perform fewer message startups but send
more data. Hence, they can be expected to be more efficient on smaller problems
and larger numbers of processors. This result can be confirmed experimentally,
as illustrated in Figure 4.6. A
flexible parallel program might incorporate all three algorithms and select the
appropriate alternative at runtime. Of course, a programming tool that supports
only sequential composition will allow only the first algorithm to be used.
The convolution problem illustrates the design tradeoffs that can arise when
constructing even relatively simple parallel programs. These tradeoffs can arise
at multiple levels. First, we must identify candidate parallel algorithms for
the component modules: in this case, the 2-D FFT. Then, we must decide how to
compose these building blocks so as to construct a complete parallel algorithm.
Aspects of the complete design in turn influence the techniques used within
components, requiring for example that we operate on columns before rows in the
inverse FFT. The performance analysis must take into account all these design
decisions.
![[DBPP]](4_4 Case Study Convolution.files/asm_color_tiny.gif)





![[Search]](4_4 Case Study Convolution.files/search_motif.gif)
Next: 4.5
Case Study: Tuple Space Up: 4
Putting Components Together Previous: 4.3
Performance Analysis
© Copyright 1995 by Ian Foster
 N , are input in
pairs on streams A and B ; convolution generates a new array
of the same size that is output on stream C (Figure 4.4). A
single convolution operation involves the transformation of two input arrays
using independent two-dimensional fast Fourier transforms (2-D FFTs), a
pointwise multiplication of the two transformed arrays, and the transformation
of the resulting array using an inverse 2-D FFT, thereby generating an output
array. A 2-D FFT performs 1-D FFTs first on each row and then on each column of
an array. A 1-D Fourier transform,
N , are input in
pairs on streams A and B ; convolution generates a new array
of the same size that is output on stream C (Figure 4.4). A
single convolution operation involves the transformation of two input arrays
using independent two-dimensional fast Fourier transforms (2-D FFTs), a
pointwise multiplication of the two transformed arrays, and the transformation
of the resulting array using an inverse 2-D FFT, thereby generating an output
array. A 2-D FFT performs 1-D FFTs first on each row and then on each column of
an array. A 1-D Fourier transform, 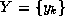 , of a sequence of N
values,
, of a sequence of N
values, 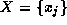 , is given by
, is given by
![[DBPP]](4_4 Case Study Convolution.files/asm_color_tiny.gif)





![[Search]](4_4 Case Study Convolution.files/search_motif.gif)
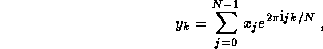
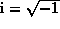 . The FFT exploits symmetry to
perform this computation in
. The FFT exploits symmetry to
perform this computation in 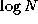 steps, each involving
steps, each involving 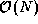 operations.
operations.


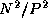 to each of the P-1 other processors. Hence, total communication costs
summed over P processors are
to each of the P-1 other processors. Hence, total communication costs
summed over P processors are
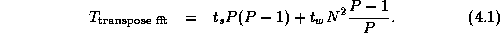
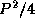 messages. The entire array is
communicated. Hence, total communication costs are
messages. The entire array is
communicated. Hence, total communication costs are
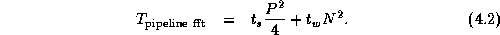
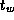 are small or when P
or
are small or when P
or 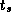 are large. On the other hand,
the first algorithm probably incurs lower data transfer costs and hence may be
superior in other situations.
are large. On the other hand,
the first algorithm probably incurs lower data transfer costs and hence may be
superior in other situations.
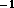 calls invoking the
transpose 2-D parallel FFT.
calls invoking the
transpose 2-D parallel FFT.
 = fft(A)
= fft(A)
 = fft(B)
= fft(B)
 = A
= A .B
.B
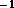 (C
(C )
)
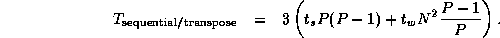
 rather than
rather than 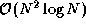
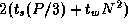 is required
to move data from the processors handling the forward FFTs to the processors
handling the inverse FFT.
is required
to move data from the processors handling the forward FFTs to the processors
handling the inverse FFT.