
![[DBPP]](10_3 Distributed Random Generators.files/asm_color_tiny.gif)





![[Search]](10_3 Distributed Random Generators.files/search_motif.gif)
The techniques described here for constructing distributed random number generators are based on an adaptation of the linear congruential algorithm called the random tree method. We first show how this method can be applied to a single generator to construct a tree of generators in a deterministic and reproducible fashion. This facility is particularly valuable in computations that create and destroy tasks dynamically during program execution.
The random tree method employs two linear congruential generators, L and R , that differ only in the values used for a .

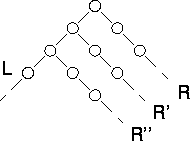
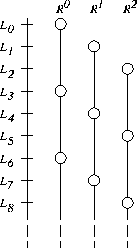
Figure
10.1: The random tree method. Two generators are used to construct
a tree of random numbers. The right generator is applied to elements of the
sequence L generated by the left generator to generate new sequences
R , R' , R'' , etc.
Application of the left generator L to a
seed  generates one random
sequence; application of the right generator R to the same seed
generates a different sequence. By applying the right generator to elements of
the left generator's sequence (or vice versa), a tree of random numbers can be
generated. By convention, the right generator R is used to generate
random values for use in computation, while the left generator L is
applied to values computed by R to obtain the starting points
generates one random
sequence; application of the right generator R to the same seed
generates a different sequence. By applying the right generator to elements of
the left generator's sequence (or vice versa), a tree of random numbers can be
generated. By convention, the right generator R is used to generate
random values for use in computation, while the left generator L is
applied to values computed by R to obtain the starting points  ,
,  ,
etc., for new right sequences (Figure 10.1).
,
etc., for new right sequences (Figure 10.1).
The strength of the random tree method is that it can be used to generate new random sequences in a reproducible and noncentralized fashion. This is valuable, for example, in applications in which new tasks and hence new random generators must be created dynamically. Before creating a new task, a parent task uses the left generator to construct a new right generator, which it passes to its new offspring. The new task uses this right generator to generate the random numbers required for its computation. If it in turn must generate a new task, it can apply the left generator to its latest random value to obtain a new random seed.
A deficiency of the random tree method as described here is that there is no
guarantee that different right sequences will not overlap. The period of
R is usually chosen to be near to m , because this maximizes
the quality of the random numbers obtained by using the generator. Hence, the
starting points 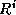 returned by the left
generator are likely to be different points in the same sequence, in which case
we can think of L as selecting random starting points in the sequence
constructed by R . If two starting points happen to be close to each
other, the two right sequences that are generated will be highly correlated.
returned by the left
generator are likely to be different points in the same sequence, in which case
we can think of L as selecting random starting points in the sequence
constructed by R . If two starting points happen to be close to each
other, the two right sequences that are generated will be highly correlated.
In some circumstances, we may know that a program requires a fixed number of generators. (For example, we may require one generator for each task in a domain decomposition algorithm.) In this case, a variant of the random tree method called the leapfrog method can be used to generate sequences that can be guaranteed not to overlap for a certain period.
Let n be the number of sequences required. Then we define 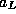 and
and 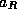 as a and
as a and
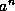 , respectively, so
that we have
, respectively, so
that we have

Then, we create n different right generators 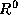 ..
..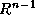 by
taking the first n elements of L as their starting values. The
name ``leapfrog method'' refers to the fact that the i th sequence
by
taking the first n elements of L as their starting values. The
name ``leapfrog method'' refers to the fact that the i th sequence 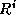 consists of
consists of 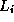 and every n
th subsequent element of the sequence generated by L (Figure 10.2). As
this method partitions the elements of L , each subsequence has a
period of at least P/n , where P is the period of L .
(If n divides P , then the period of a subsequence is exactly
P/n .) In addition, the n subsequences are disjoint for their
first P/n elements.
and every n
th subsequent element of the sequence generated by L (Figure 10.2). As
this method partitions the elements of L , each subsequence has a
period of at least P/n , where P is the period of L .
(If n divides P , then the period of a subsequence is exactly
P/n .) In addition, the n subsequences are disjoint for their
first P/n elements.
Figure
10.2: The leapfrog method with n=3 . Each of the three
right generators selects a disjoint subsequence of the sequence constructed by
the left generator's sequence.
The generator for the r th subsequence,  , is defined
by
, is defined
by 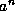 and
and 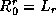 . We can compute
these values as follows. We first compute
. We can compute
these values as follows. We first compute 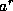 and
and 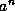 ; these computations
can be performed in
; these computations
can be performed in 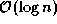 time by taking
advantage of the identity
time by taking
advantage of the identity
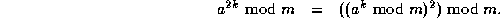
We then compute members of the sequence 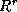 as follows, to
obtain n generators, each defined by a triple
as follows, to
obtain n generators, each defined by a triple 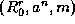 , for
, for 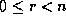 .
.

The leapfrog method can be applied recursively: the subsequence corresponding
to a generator 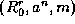 can be further
subdivided by a second application of the leapfrog method. Doing this can be
useful when random numbers are required at several levels in a task hierarchy.
However, the periods of the resulting sequences become shorter, and their
statistical properties are less certain.
can be further
subdivided by a second application of the leapfrog method. Doing this can be
useful when random numbers are required at several levels in a task hierarchy.
However, the periods of the resulting sequences become shorter, and their
statistical properties are less certain.
In other situations, we may know the maximum number, n , of random values needed in a subsequence but not the number
of subsequences required. In this case, a variant of
the leapfrog method can be used in which the role of L and R
are reversed so that the elements of subsequence i are the contiguous
elements 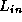 ..
..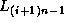 (Figure 10.3), as
follows:
(Figure 10.3), as
follows:

It is not a good idea to choose n as a power of two, as this can lead to serious long-term correlations.
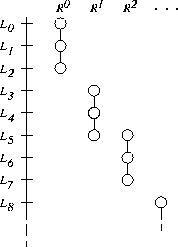
Figure
10.3: Modified leapfrog with n=3 . Each subsequence
contains three contiguous numbers from the main sequence.
![[DBPP]](10_3 Distributed Random Generators.files/asm_color_tiny.gif)





![[Search]](10_3 Distributed Random Generators.files/search_motif.gif)
© Copyright 1995 by Ian Foster